IMPRESSIVE RESUMES EASY ONLINE BUILDER
- Professional out-of-the-box resumes, instantly generated by the most advanced resume builder technology available.
- Effortless crafting. Real-time preview & pre-written resume examples.
Dozens of HR-approved resume templates. - Land your dream job with the perfect resume employers are looking for!
Millions have won jobs at top companies thanks to our resume maker
3 EASY STEPS TO CREATE YOUR PERFECT RESUME
CHOOSE YOUR
RESUME TEMPLATE
Our professional resume templates are designed strictly following all industry guidelines and best practices that employers look for.
SHOW WHAT
YOU'RE MADE OF
Not finding the right words to showcase yourself? We´ve added thousands of pre-written examples and resume samples. As easy as clicking.
DOWNLOAD
YOUR RESUME
Start impressing employers. Download your awesome resume and land the job you are looking for, effortlessly.
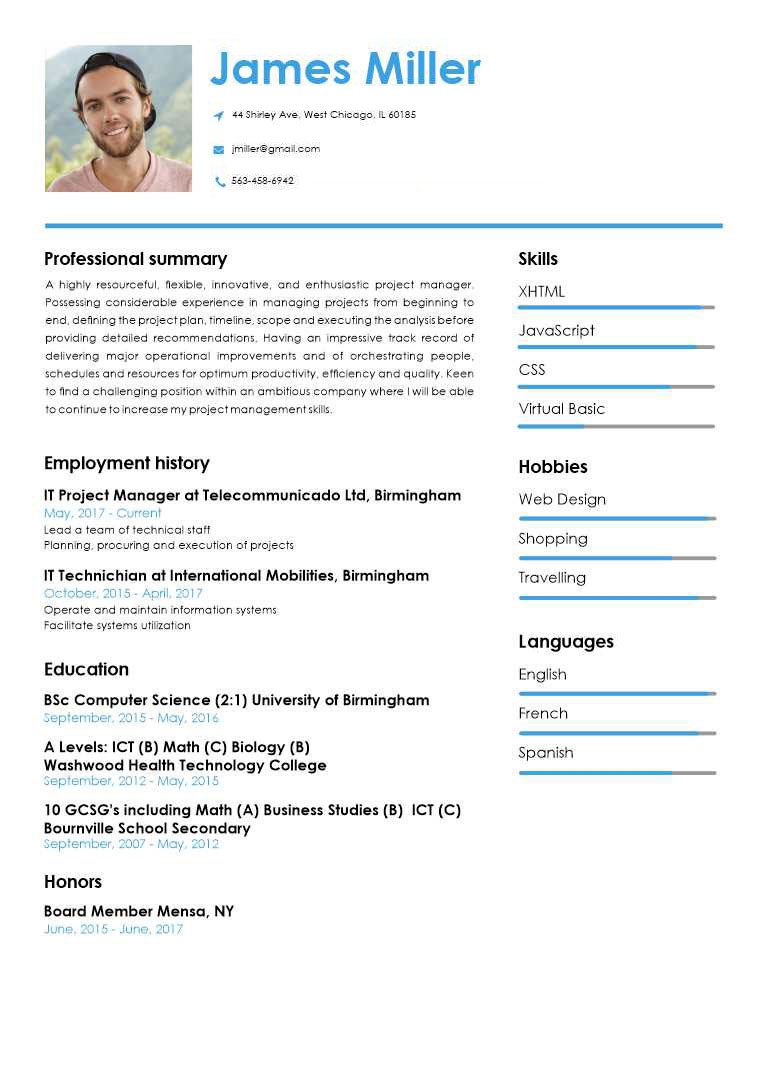
PROFESSIONAL RESUME TEMPLATES
people like you the jobs they were dreaming of.

How to Make a Resume?
- Select your favorite template.
- Add your contact information.
- Fill out your work history and education.
- Select from our hundreds of job descriptions and skill examples, or input your own!
- Review your resume & download it.
THE RAGE IS ALL ABOUT US
Mia Cooper
Easy to follow prompts and beautiful templates to choose from!! Started getting calls for job interviews a few days after submitting and applying the resume that I created with the help of this amazing website. It definitely stands out!
George Holand
Found this website really very helpful since I wanted to make my resume look super professional and eye-catching too…Finally, I was able to set up a perfect resume!!!
Allison Doman
Download took 2-3 seconds…..I made my CV while waiting in the queue to attend my interview! I loved the professional resume templates. Thanks for this useful website.
Camille Ryan V
Went for a job interview and the potential employers were very impressed with my CV. I must say that Resumebuild comes with so many interesting templates and also, creating a resume with it is super easy.
 Have Questions About Writing A Great Resume?
Have Questions About Writing A Great Resume?
Expert Answers to All Your Resume Inquiries.
Resume Templates FAQ
A resume, sometimes called a CV or curriculum vitae, is a document mostly used to showcase your career background, skills, and accomplishments when searching for a job. Resume Build helps you create professional resumes tailored to the specific industry or job you want in just minutes.
Resume Build has hundreds of resume templates and pre-written resume examples divided by industry, experience level, and careers. Just follow the simple steps to make a high school resume to help you land your first job in a few minutes.
Resume Build helps you make a job-winning resume on any device with just a few clicks. Follow the easy instructions and start by choosing the template you need for our library of professionally designed resume templates by industries, to create a perfect resume on your phone or computer fast.
Resumes should grab the recruiter’s attention in just a few seconds, and Resume Build helps you create the perfect resume using expert tips and pre-written resume examples to build it fast and easily. While the length of the resume depends on the career field and experience of the applicant, a two-page resume is ideal, according to employers.
Resume Build is the simplest resume builder available online to help you create job-winning resumes in no time. Use Resume Build now to create a professional resume for free by just following a few simple steps. Choose from hundreds of industry-specific resume templates and use our pre-written resume examples targeted by job or by careers to make a perfect resume in just a few minutes.